2019年河南高考文科数学模拟试卷【附答案】

知识问答 2022-01-08 19:12:58 admin

2019年河南高考文科数学模拟试卷【附答案】

一、选择题（本大题共12小题，共60.0分）

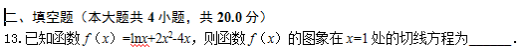
答案和解析

1.【答案】B
【解析】

解：∵
故选：B．
本题是一个复数的乘除运算，先进行复数乘法运算，在分子和分母上进行，再进行复数的除法运算，分子和分母同乘以分母的共轭复数，化简后得到结果．
本题考查复数的乘除混合运算，是一个基础题，复数的加减乘除运算是比较简单的问题，在高考时有时会出现，若出现则是要我们一定要得分的题目．

2.【答案】D
【解析】

解：将集合M和集合N中的方程联立得：

将集合M与集合N中的方程联立组成方程组，求出方程组的解即可确定出两集合的交集．
此题考查了交集及其运算，以及二元一次方程组的解法，是一道基本题型，学生易弄错集合中元素的性质．

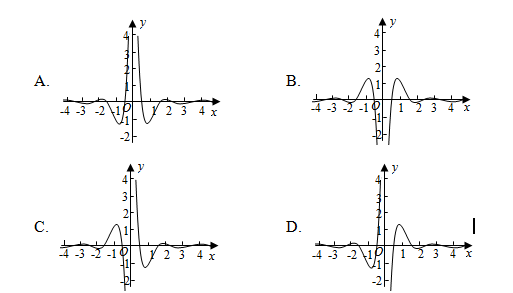
3.【答案】A
【解析】

解：定义域为（-∞，0）∪（0，+∞），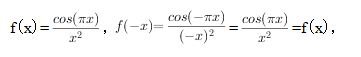

∴f（-x）=f（x），f（x）为偶函数，．
∴其图象关于y轴对称，可排除C，D；
又当x→0时，cos（πx）→1，x2→0，
∴f（x）→+∞．故可排除B；
而A均满足以上分析．
故选：A．
由于函数为偶函数，其图象关于y轴对称，可排除C、D，利用极限思想（如x→0+，y→+∞）可排除B，从而得到答案A．
本题考查奇偶函数图象的对称性，考查极限思想的运用，考查排除法的应用，属于中档题．

4.【答案】D
【解析】

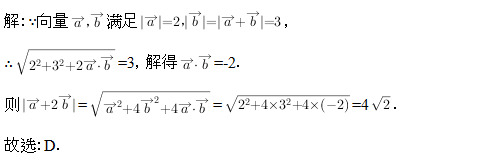
利用数量积运算性质即可得出．
本题考查了数量积运算性质，考查了推理能力与计算能力，属于基础题．

5.【答案】A
【解析】

根据题意，设要求双曲线的方程为，将点（2，-2）代入双曲线的方程，计算可得t的值，将t的值代入双曲线的方程，变形即可得答案．
本题考查双曲线的几何性质，关键是掌握有共同渐近线方程的双曲线方程的特点．

6.【答案】A
【解析】

由已知及余弦定理可求a，b的值，进而根据三角形的面积公式即可计算得解．
本题主要考查了余弦定理，三角形的面积公式在解三角形中的综合应用，属于基础题．

7.【答案】B
【解析】

解：模拟程序的运行，可得
S=0，i=1
执行循环体，S=290，i=2
不满足判断框内的条件，执行循环体，S=300，i=3
不满足判断框内的条件，执行循环体，S=310，i=4
不满足判断框内的条件，执行循环体，S=320，i=5
不满足判断框内的条件，执行循环体，S=330，i=6
不满足判断框内的条件，执行循环体，S=340，i=7
不满足判断框内的条件，执行循环体，S=350，i=8
由题意，此时，应该满足判断框内的条件，退出循环，输出S的值为350．
可得判断框中的条件为i＞7？．
故选：B．
由已知中的程序语句可知：该程序的功能是利用循环结构计算并输出变量S的值，模拟程序的运行过程，分析循环中各变量值的变化情况，可得答案．
本题考查了程序框图的应用问题，解题时应模拟程序框图的运行过程，以便得出正确的结论，是基础题．

8.【答案】D
【解析】

故选：D．
甲、乙二人抢到的金额之和包含的基本事件总数n==10，甲、乙二人抢到的金额之和不低于3元包含的基本事件有6个，由此能出甲、乙二人抢到的金额之和不低于3元的概率．
本题考查概率的求法，考查古典概型概率计算公式等基础知识，考查运算求解能力，考查函数与方程思想，是基础题．

9.【答案】B
【解析】

故选：B．
以A为坐标原点，建立空间直角坐标系，求出与的坐标，利用数量积求夹角公式求解．
本题考查异面直线所成角，训练了两角空间向量求解空间角，是基础题．

10.【答案】B
【解析】

利用函数y=Acos（ωx+φ）的图象变换规律，余弦函数的图象的对称性，求得φ的值．
本题主要考查函数y=Acos（ωx+φ）的图象变换规律，余弦函数的图象的对称性，属于基础题．

11.【答案】C
【解析】

13.【答案】x-y-3=0
【解析】

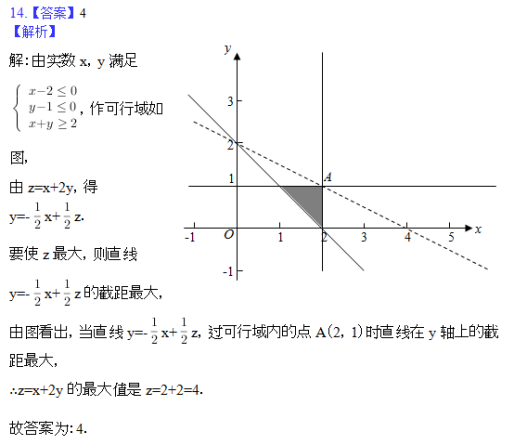由约束条件作出可行域，化目标函数为直线方程的斜截式，由图看出使目标函数取得最大值的点，求出点的坐标，代入目标函数得答案．
本题考查简单的线性规划，考查了数形结合的解题思想方法，是中档题．

将已知等式两边平方后相加，根据同角三角函数基本关系式，两角和的正弦函数公式即可计算得解．
本题主要考查了同角三角函数基本关系式，两角和的正弦函数公式在三角函数化简求值中的应用，属于基础题．

【解析】

（1）通过离心率以及短轴长，求出b，a得到椭圆方程，通过抛物线的焦点坐标求解抛物线方程即可．
本题考查椭圆以及抛物线的简单性质的应用，方程的求法，直线与椭圆的位置关系的综合应用，考查转化思想以及计算能力．

【解析】

（1）构造函数g（x）=f（x）-x+1，求函数的导数，研究的单调性和极值，结合函数极值和最值进行求解即可．
（2）利用参数分离法，构造函数，求函数的导数，研究函数的最值进行求解即可．
本题主要考查导数与不等式的应用以及函数最值的求解，求函数的导数，利用参数分离法转化为求函数的最值是解决本题的关键．

【解析】