黑龙江省2019年高考文科数学模拟试题【含答案】
![]()
黑龙江省2019年高考文科数学模拟试题【含答案】
一、选择题(本大题共12小题,共60.0分)
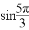 =( )
=( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
- 已知集合A={x|x<1},B={x|3x<1},则( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
- 设Sn为等比数列{an}的前n项和,若8a2+a5=0,则
 等于( )
等于( )
A. 11 B. ![]() C.
C. ![]() D. 5
D. 5
- 下列函数中,其定义域和值域分别与函数y=10lgx的定义域和值域相同的是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
- 已知
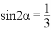 ,则
,则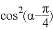 =( )
=( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
- 函数f(x)=ln(x2-4x+3)的单调递增区间是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
- 记Sn为等差数列{an}的前n项和.若3S3=S2+S4,a1=2,则a5=( )
A. ![]() B.
B. ![]() C. 10 D. 12
C. 10 D. 12
- 已知x0=
 是函数f(x)=sin(2x+φ)的一个极大值点,则f(x)的一个单调递减区间是( )
是函数f(x)=sin(2x+φ)的一个极大值点,则f(x)的一个单调递减区间是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
- 已知{an}为等比数列,a4+a7=2,a5a6=-8,则a1+a10=( )
A. 7 B. 5 C. ![]() D.
D. ![]()
- 将函数y=sin(2x-
 )图象向左平移
)图象向左平移 个单位,所得函数图象的一条对称轴的方程是( )
个单位,所得函数图象的一条对称轴的方程是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
- 已知函数f(x)=
 ,x∈R,若对任意θ∈(0,
,x∈R,若对任意θ∈(0,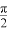 ],都有f(msinθ)+f(1-m)>0成立,则实数m的取值范围( )
],都有f(msinθ)+f(1-m)>0成立,则实数m的取值范围( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
- 已知函数f(x)=xlnx-aex(e为自然对数的底数)有两个极值点,则实数a的取值范围是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
二、填空题(本大题共4小题,共20.0分)
- 已知数列{an}满足
 ,
,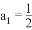 ,则a2019=______
,则a2019=______ - 记Sn为数列{an}的前n项和,若Sn=2an+1,则an=______
- △ABC的内角A,B,C的对边分别为a,b,c,若cosA=
 ,cosC=
,cosC=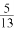 ,a=1,则b=______.
,a=1,则b=______. - 已知函数f(x)=2cosx+sin2x,则f(x)的最小值是______
三、解答题(本大题共7小题,共82.0分)
- 在△ABC中,角A,B,C所对的边分别为a,b,c,已知
 .
.
(1)求角B的大小;
(2)若b= ,a+c=3,求△ABC的面积.
,a+c=3,求△ABC的面积.
- 已知函数f(x)=sin2ωx+
 sinωx•sin(ωx+
sinωx•sin(ωx+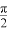 )(ω>0)的最小正周期为π.
)(ω>0)的最小正周期为π.
(1)求ω的值;
(2)求函数f(x)在区间[0, ]上的取值范围.
]上的取值范围.
- 设数列{an}的前n项和为Sn,点
 均在函数y=x+2的图象上.
均在函数y=x+2的图象上.
(1)求数列{an}的通项公式;
(2)设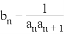 ,Tn是数列{bn}的前n项和,求使得
,Tn是数列{bn}的前n项和,求使得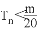 对所有n∈N*都成立的最小正整数m.
对所有n∈N*都成立的最小正整数m.
- 已知椭圆C:
 +
+ =1(a>b>0)经过点M(1,
=1(a>b>0)经过点M(1,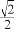 ),其离心率为
),其离心率为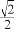 ,设直线l:y=kx+m与椭圆C相交于A、B两点.
,设直线l:y=kx+m与椭圆C相交于A、B两点.
(1)求椭圆C的方程;
(2)已知直线l与圆x2+y2= 相切,求证:OA⊥OB(O为坐标原点).
相切,求证:OA⊥OB(O为坐标原点).
- 已知函数f(x)=ax-lnx(a∈R).
(1)求函数f(x)的单调区间;
(2)若函数f(x)有两个零点,x1,x2,证明 +
+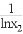 >2.
>2.
- 在平面直角坐标系xOy中,直线l的参数方程为
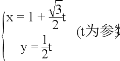 ,以坐标原点O为极点,x轴的非负半轴为极轴建立极坐标系,圆C的极坐标方程为ρ=-4cosθ.
,以坐标原点O为极点,x轴的非负半轴为极轴建立极坐标系,圆C的极坐标方程为ρ=-4cosθ.
(1)求圆C的圆心到直线l的距离;
(2)已知P(1,0),若直线l与圆C交于A,B两点,求 的值.
的值.
- 已知函数f(x)=|x-2|+2,g(x)=m|x|(m∈R).
(1)解关于x的不等式f(x)>5;
(2)若不等式f(x)≥g(x)对任意x∈R恒成立,求m的取值范围.
答案和解析
1.【答案】C
【解析】
解:![]() =sin(2π-
=sin(2π-![]() )=-sin
)=-sin![]() =-
=-![]() .
.
故选:C.
利用诱导公式,特殊角的三角函数值即可化简求值得解.
本题主要考查了诱导公式,特殊角的三角函数值在三角函数化简求值中的应用,考查了转化思想,属于基础题.
2.【答案】A
【解析】
解:∵集合A={x|x<1},
B={x|3x<1}={x|x<0},
∴A∩B={x|x<0},故A正确,D错误;
A∪B={x|x<1},故B和C都错误.
故选:A.
先分别求出集合A和B,再求出A∩B和A∪B,由此能求出结果.
本题考查交集和并集求法及应用,是基础题,解题时要认真审题,注意交集、并集定义的合理运用.
3.【答案】B
【解析】
解:设公比为q,
由8a2+a5=0,得8a2+a2q3=0,q3=-8,解得q=-2,
所以![]() =
=![]() ═-11,
═-11,
故选:B.
设公比为q,由8a2+a5=0可求得q值,利用前n项和公式表示出S2,S5即可求得![]() 的值.
的值.
本题主要考查等比数列的通项公式与前n项和公式,考查学生的计算能力,属中档题.
4.【答案】D
【解析】
解:函数y=10lgx的定义域和值域均为(0,+∞),
函数y=x的定义域和值域均为R,不满足要求;
函数y=lgx的定义域为(0,+∞),值域为R,不满足要求;
函数y=2x的定义域为R,值域为(0,+∞),不满足要求;
函数y=![]() 的定义域和值域均为(0,+∞),满足要求;
的定义域和值域均为(0,+∞),满足要求;
故选:D.
分别求出各个函数的定义域和值域,比较后可得答案.
本题考查的知识点是函数的定义域和值域,熟练掌握各种基本初等函数的定义域和值域,是解答的关键.
5.【答案】C
【解析】
解:∵![]() ,
,
∴cos(2α-![]() )=
)=![]() ,
,
∴cos[2(α-![]() )]=
)]=![]() ,
,
∴2cos2(α-![]() )-1=
)-1=![]() ,
,
∴cos2(α-![]() )=
)=![]()
故选:C.
首先,结合诱导公式,然后,根据二倍角公式求解即可.
本题重点考查了二倍角的余弦公式、诱导公式等知识,属于基础题.
6.【答案】D
【解析】
解:令t=x2-4x+3=(x-1)(x-3)=(x-2)2-1>0,求得x<1,或x>3,故函数的定义域为{x|x<1,或x>3 },
f(x)=g(t)=lnt,
故本题即求函数g(t)在定义域上的增区间.
再利用二次函数的性质可得g(t)在定义域上的增区间为(3,+∞),
故选:D.
令t=x2-4x+3>0,求得函数的定义域,再由f(x)=lnt,可得本题即求函数t在定义域上的增区间,再利用二次函数的性质可得t在定义域上的增区间.
本题主要考查复合函数的单调性,二次函数的性质,体现了转化的数学思想,属于基础题.
7.【答案】B
【解析】
解:∵Sn为等差数列{an}的前n项和,3S3=S2+S4,a1=2,
∴![]() =a1+a1+d+4a1+
=a1+a1+d+4a1+![]() d,
d,
把a1=2,代入得d=-3
∴a5=2+4×(-3)=-10.
故选:B.
利用等差数列的通项公式和前n项和公式列出方程,能求出a5的值.
本题考查等差数列的第五项的求法,考查等差数列的性质等基础知识,考查运算求解能力,考查函数与方程思想,是基础题.
8.【答案】B
【解析】
解:∵x0=![]() 是函数f(x)=sin(2x+φ)的一个极大值点,
是函数f(x)=sin(2x+φ)的一个极大值点,
∴sin(2×![]() +φ)=1,∴2×
+φ)=1,∴2×![]() +φ=2kπ+
+φ=2kπ+![]() ,解得φ=2kπ-
,解得φ=2kπ-![]() ,k∈Z,
,k∈Z,
不妨取φ=-![]() ,此时f(x)=sin(2x-
,此时f(x)=sin(2x-![]() )
)
令2kπ+![]() <2x-
<2x-![]() <2kπ+
<2kπ+![]() 可得kπ+
可得kπ+![]() <x<kπ+
<x<kπ+![]() ,
,
∴函数f(x)的单调递减区间为(kπ+![]() ,kπ+
,kπ+![]() )k∈Z,
)k∈Z,
结合选项可知当k=0时,函数的一个单调递减区间为(![]() ,
,![]() ),
),
故选:B.
由极值点可得φ=-![]() ,解2kπ+
,解2kπ+![]() <2x-
<2x-
标签:
相关文章
发表评论

评论列表