怎样利用微分形式不变性来计算复杂函数的全微分

在学习多元函数微分学这一部分的内容时，想必大家也积累了很多求全微分、求偏导的方法，今天我的这篇指南就给大家分享:如何利用微分形式不变性来计算全微分？希望看完之后，你能对微分学有进一步深刻的理解。

操作方法

【步骤01】

咱们以下图中的一道题目为例子，显然这个函数是比较复杂的：指数与三角函数的乘积，要求我们写出全微分，并求出Z分别关于X，Y的一阶偏导数。

【步骤02】

对于复杂函数就要有换元的思想，首先令s＝xy，t＝x+y，换元处理后如下:

【步骤03】

对换元后的函数求微分就变得简单了，我们根据微分的定义:把全微分表示成为线性函数和，如图

【步骤04】

之前通过s，t换元，这里就要再对s，t两个变量写出微分表达式，如下

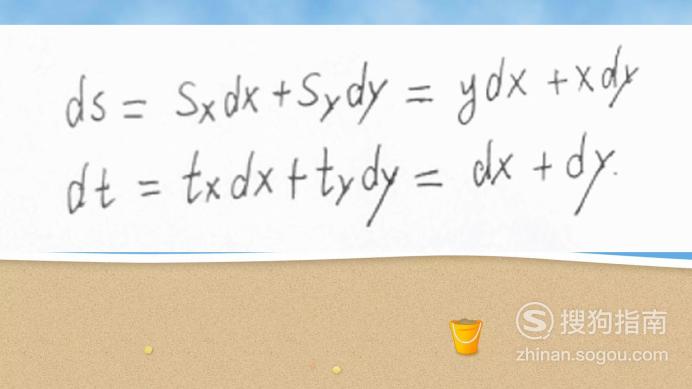
【步骤05】

现在进行回带，得到全微分dz表达式
进行整理形式要求为Adx+Bdy即可。

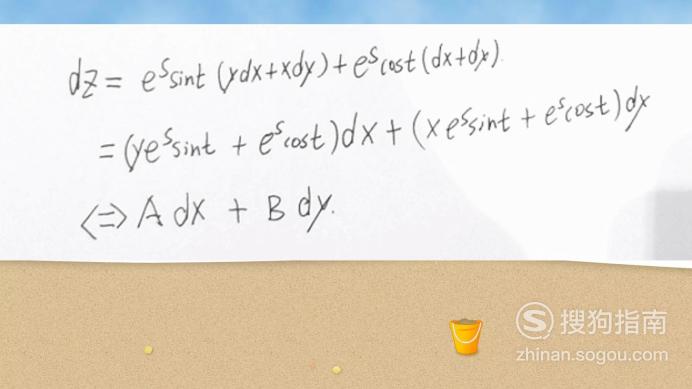
【步骤06】

最后将s＝xy，t＝x+y替换，写出关于x，y的形式，毕竟s，t是我们自己产生的中间变量，不能作为最终的结果。

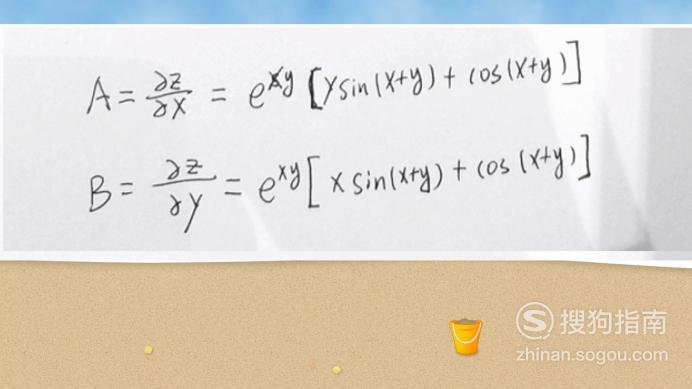
【步骤07】

【总结】:复杂函数先找到中间变量换元，一层一层地求全微分即可，最后不要忘记要用原函数的变量表示结果。