如何求数列通项公式：错项相减法

数列是高中数学中重要的组成部分，其中求数列的通项公式是考察的重要知识点之一，下面就为大家详细介绍一种求数列通项公式的方法——错项相减法。

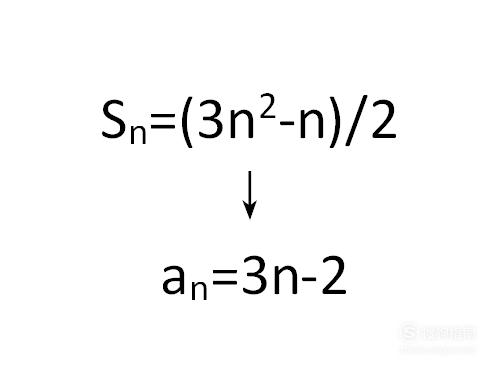
操作方法

【步骤01】

数列是有一定规律的数字的排列，若某个数列的前n项和可以用一个通用的式子表示出来，则可用错相相减法来求得该数列的通项公式，这也是用该方法的前提条件。

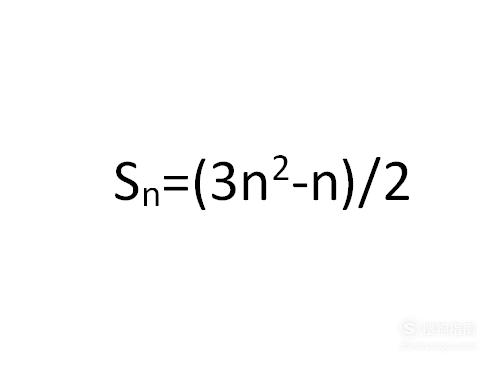
【步骤02】

在有了数列前n项和的公式后，将（n-1）项带入公式，求得该数列前（n-1）项的和。若数列前n项和用S（n）来表示，则需求出S（n-1）。

【步骤03】

再用S（n-1）-S（n），即可求得数列的第n项的表达式。若用a（n）表示数列的第n项，则a（n）=S（n-1）-S（n）（n≥2）。

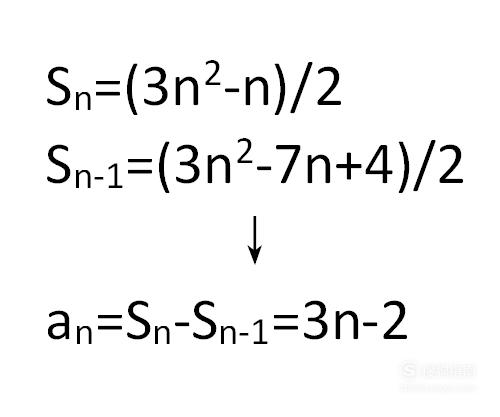
【步骤04】

在用此方法求得数列的通项公式后需用通项公式对数列第一项进行验证，因为在上述公式中，n的值必须大于等于2，故需要检查首项。首项将S（n）中的n代为1算出，检查第一项是否也满足该通项公式a（n），若不满足，则需将第一项单独写出。

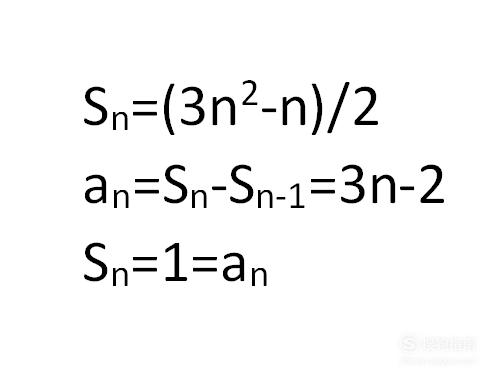
【步骤05】

在正确写出数列的通项公式后，需再写出数列的前几项，并对其进行加和，验证结果是否与用前n项和公式计算出的结果相同，若结果一致，则可基本确认算出的通项公式无误。

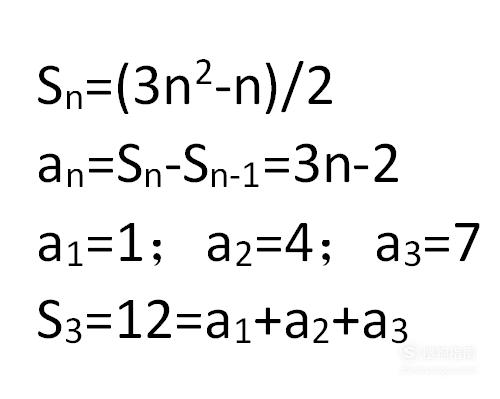
特别提示

在学习后一定要多练习，才能熟练运用该方法求数列的通项公式。