怎么运用高数中的分部积分法

积分是高数里的重要内容，而对于不同的被积函数，积分的方法也有很多。两类函数相乘得到得新的函数，对于新函数得积分如果用传统办法积分，则很难得出结果，此时便可用分部积分对其进行积分，从而快速得出积分结果。

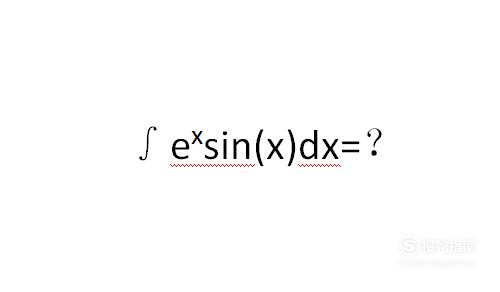
操作方法

【步骤01】

以∫(e^x)sin(x)dx为例为大家讲解这种方法。首先将sin(x)积分，然后将得到得结果放到d的后面，将整个积分式变为对（-cos(x)）积分。如下图。

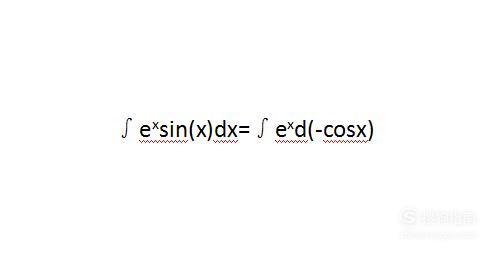
【步骤02】

接下来便将用到一个公式，即∫u(x)dv(x)=u(x)v(x)-∫v(x)du(x)。将上一步得到的结果带入此公式。

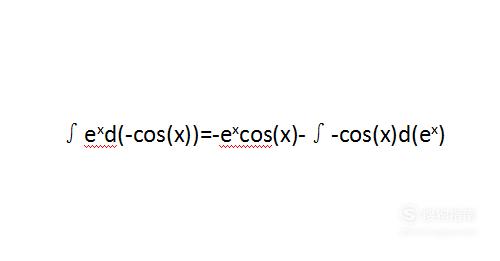
【步骤03】

将上一步得到的结果化简。

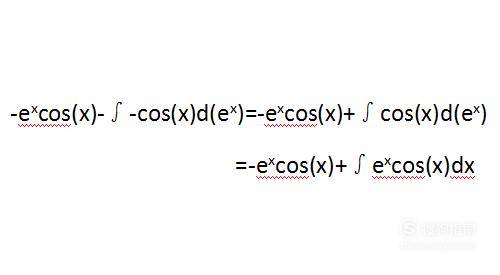
【步骤04】

再对后面的式子进行分部积分，即对∫(e^x)cos(x)dx进行分部积分，方法与上相同。先对cos(x)积分，结果放到d后面。

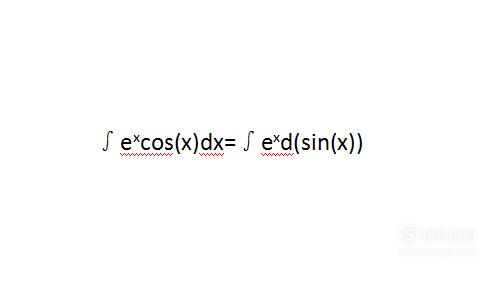
【步骤05】

再次运用步骤二中的公式,并化简，将得到一个关键的结果。

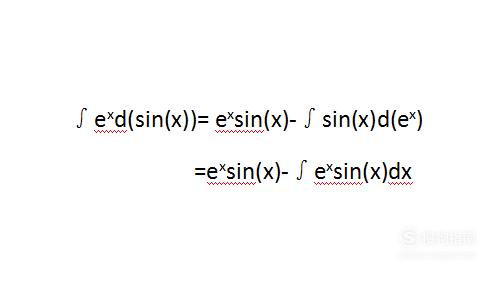
【步骤06】

将结果带回步骤三得到如下结果。

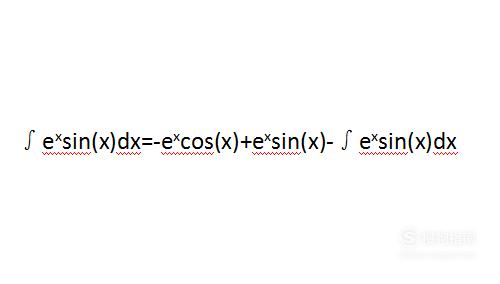
【步骤07】

通过观察，可将右边第三项移项到左边，即可得出结果。

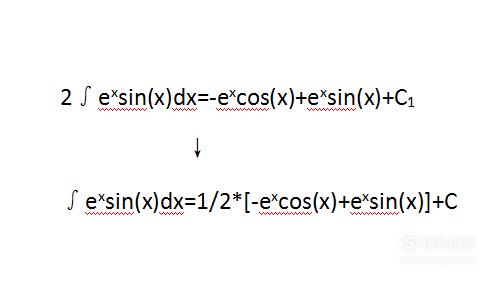
【步骤08】

最后将所有步骤合在一起，便于读者看懂过程。

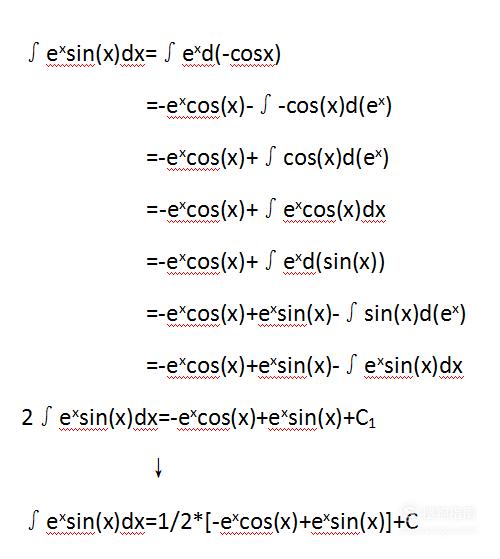
特别提示

分部积分是一个重要积分方法，一定要多加练习，熟悉这种积分方法。